Can the small comets be detected with binoculars? We have previously estimated the detection rate with telescopes owned by amateur astronomers and have shown that the detection rate is about 1 or 2 per night of clear-sky viewing, if the telescope is pointed in the proper position just after dusk and just prior to dawn. But let us take a look at the binocular situation for a range to the small comet of 1000 km (625 miles). We will use binoculars with a magnification of 7X and a clear entrance pupil of 50 mm in diameter. For the human eye, the entrance pupil varies but a diameter of 5 mm is typical. Thus the binoculars increase the light-gathering capability of the human eye by a factor of 100, or V=5. As seen through the binoculars then, the brightness of a small comet with V=8.3 is V= (8.3 - 5) = 3.3 and is detectable with the eye.
Consequently, the frequency of detection of the small comets with the binoculars is of interest. The viewing geometry is quite constrained because the objects will not be seen in the darkness of Earth's shadow and certainly not through the sunlit atmosphere. In fact, the atmospheric brightness is not less than V=3.1, and similar to the brightness of the small comet, until about 72 minutes after sunset and during the period 72 minutes before sunrise. We estimate that there are approximately 30-minute windows for detection of these small comets at solar phase angles in the range of 18 degrees to 40 degrees which are contiguous to and on the dark side of the above two windows. Importantly, the binoculars must be pointed at the intersection of Earth's shadow and the 1000-km (625-mile) range. The apparent motions of the small comets will be in the range of about 1 degree/s and will remain in the field-of-view of binoculars with a field-of-view of 10 degrees for about 10 seconds.
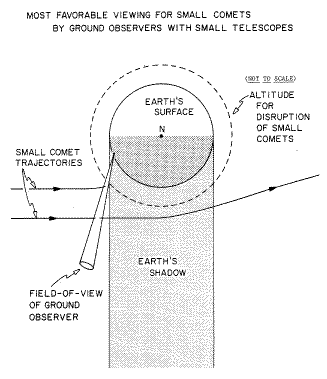Now we must calculate the frequency of the small comet detections with
your binoculars. The viewing is through the Earth's shadow so that part
of the detection area must be subtracted because, obviously, if the sun
doesn't shine on the comets they are essentially invisible.(See the
viewing geometry in the accompanying drawing.) With an apex at your
binoculars and the two lines extending to 1000 km (625 miles), a rough
estimate of the area in sunlight is approximately 2/3 of the total area
of the triangle. If your field-of-view is 10 degrees then the detection
area in sunlight is about 6 x 104
km2. For the present purposes of simple
estimation we use the average interplanetary rate of 1.2 x
10-9 small
comets/km2-s intercepting the above detection
area and neglect the effects of Earth's gravitational focusing. Thus the
detection rate is about (1.2 x 10-9) x (6 x
104) = 7 x 10-5
events/s, or 1 event every 5 hours. Since your viewing time is about 30
minutes each for the pre-dawn and post-dusk samples, one would expect to
see one event every 5 days of viewing with these binoculars. The short
period for viewing is due to the rotation of the Earth and the rapid
geometric degradation of the viewing geometry.
For telescopes with larger apertures the viewing geometry remains the same as shown in the accompanying figure. The viewing geometry is generally parallel to the ecliptic plane. Basically, you can estimate your detection rate by comparing your telescope's characteristics with those for the binoculars as given above. For example, if you have a collecting aperture of 90-mm diameter, then the range of your telescope is approximately proportional to the diameter, or about 1800 km (1125 miles), since the object brightness decreases as r-2. At this distance, for an object with an apparent speed of 10 km/s, the apparent angular speed is about 0.3 degree/second. The event rate is proportional to the fan collecting area, i.e., proportional to the square of the above range times the viewing angle of your telescope. If the field-of-view of your telescope is the same as that of the above binoculars (probably smaller) then your event rate will be (1800/1000)2 x (10/10) = 3.2 greater than with the binoculars. This is about 1 event every 1.5 hours for the average interplanetary rate. The occurrence frequency is greater than this average for the months of June through the first week of November due to seasonal variations by factors in the range of 2 to 3. The rates are lesser for the other months with January at the minimal rates.